丟番圖主要數學著作《算術》 

比較確切知道的是丟番圖有兩部著作，一是《算術》，大部分保存了下來；另一個是《多角數》，只有少部分留下來。另外在《算術》中幾次提到過的是《推論集》，可能是若干數論問題的獨立匯編，也可能是附屬在《算術》中的失傳部分。此外，伊安布利霍斯（約公元250—約330年）所著《尼科馬霍斯〈算術〉評注》一書的注釋者還提到丟番圖的另外一本書《分數算法》，是討論有關分數計算方法的，可惜已失傳。

《算術》是丟番圖最重要的著作，也是代數史上的一部影響深遠的著作。它在歷史上影響之大可以和歐幾里得《幾何原本》一比高下。這書的序中說，全書共有13卷。保留至今天的只有6 卷。相傳其余7 卷在10世紀以前已經失傳。5世紀時希帕提婭（Hypatia）注釋這部書，只注了6卷，這也許是其余各卷被人忽視最終失傳的原因。       

最早具有代數學特征的著作　

希臘時代“算術”一詞，主要指“數的理論”，即相當于現在的“數論”。而數字的加、減、乘 、除等運算則叫做“計算的技巧”，兩者有明顯的區別。這種分法從畢達哥拉斯時代開始，一直延續到近代，如高斯的數論名著就叫做《算術研究》（1801）。

丟番圖《算術》是講數論的，它討論了一次、二次以及個別的三次方程，還有大量的不定方程。現在對于具有整系數的不定方程，如果只考慮其整數解，這類方程就叫做丟番圖方程。它是數論的一個分支。不過丟番圖并不要求解答是整數而只要求是正有理數。　　

從另一個角度看，《算術》一書也可以歸入代數學的范圍。代數學區別于其他學科的最大特點是引入了未知數，并對未知數加以運算，根據問題的條件列出方程，然后解方程求出未知數。

《算術》也有未知數，這未知數一般就是問題的答案，一切運算只允許對已知數來施行。在代數中既然要對未知數加以運算，就需要用某種符號來表示它。從引入未知數，創設未知數符號以及建立方程的思想（雖然未有現代方程的形式）這幾方面來看，丟番圖《算術》完全可以算得上是代數。當時代數學沒有專門的名稱，algebra是9世紀花拉子米以后才出現的名詞，而且直到17世紀還沒被歐洲人普遍接受。在《算術》中，丟番圖采用了一套數學符號來表示未知量 ，他也是首位用符號來表示冪的數學家。丟番圖將這方面的成果冠以算術之名是很自然的。他被后人稱為“代數學之父”也是有一定道理的。

《算術》以問題集的形式收錄了290個題目，其中希臘文本189個，阿拉伯文本101個，此外還有十幾個引理和推論，合起來共三百多個問題。大體上按由易到難排列，但很難看得出是用什么標準來分類的。解題的方法也是五花八門，沒有一定的法則。數學史家漢克爾(Hankel，1839—1873)說：“近代數學家研究了丟番圖的100個題后，去解101個題，仍然感到困難。……丟番圖使人眼花繚亂甚于使人欣喜”。這話稍嫌夸張，卻抓住了問題的要害。丟番圖沒有著力去探求一般性的解法，或去研究多種解法之間的內在聯系，這是《算術》的最大缺點。

 “丟番圖對代數學的發展起了極其重要的作用。”—— 伊夫斯

希臘數學自畢達哥拉斯學派以后，興趣中心在幾何，他們認為只有經過幾何論證的命他才是可靠的。為了邏輯的嚴密性，代數也披上了幾何的外衣，一切代數問題，甚至簡單的一次方程的求解，也都納入僵硬的幾何模式之中。直到丟番圖，才把代數解放出來，擺脫了幾何的羈絆。

 例如，(a＋b)²=a²+2ab＋b²的關系，在歐幾里得《幾何原本》中是一條重要的幾何定理(卷Ⅱ命題4)，而在丟番圖《算術》中只是簡單代數運算法則的必然結果。　

人們認為《算術》是希臘數學的劃時代杰作。《算術》的核心內容是關于以代數手法解方程和不定方程的研究。這里的方法不依賴于幾何證明。關于整系數方程的整數解的研究是當今數學的一個分支。這一分支被稱之為丟番圖方程。尋找畢達哥拉斯的三元組就是一個這樣的例子。丟番圖還使用了介于文體和完全的符號代數之間的一種過渡性的代數符號體系。阿拉伯數學家把《算術》翻譯成了阿拉伯語并加以廣泛研究。

丟番圖在解題過程中使用了許多高超的技巧，可以說在希臘數學中是獨樹一幟。有的數學史家說，如果丟番圖的著作不是用希臘文寫的，人們就不會想到這是希臘人的成果，因為看不出有古典希臘數學的風格，從思想方法到整個科目結構都是全新的。如果沒有丟番圖的工作，也許人們以為希臘人完全不懂代數。有人甚至猜想他是希臘化了的巴比倫人。

費馬感興趣的公式

在《算術》第2卷的第8題是關于不定方程的：將一個已知的平方數分為兩個平方數。例如將16分成兩個平方數。設一個平方數是x²，那么另一個是16-x²，現要求16-x²是一平方數。即16-x²=M²不妨設M=mx-4，其中m是某一整數，而4是16的平方根。例如令m=2，于是16-x²=4x²-16x+16，立刻得到x=16/5 。

 前面已經提到，費馬對這一命題很感興趣，在旁邊的空白處寫下著名的“費馬大定理”。大約是在 1637年左右，費馬在看到這個題目：“將一個平方數分為兩個平方數”時，在書頁的空白處寫出了著名的“費馬大定理”。1670年費馬的兒子將他父親的全部批注插入正文，重新出版巴歇的希-拉對照本近代，不包括新發現4卷的“丟番圖全集”，標準版本是唐內里（Tannery，1843—1904，法國數學史家）編輯、校訂的希-拉對照本《亞歷山大的丟番圖全集，包括希臘文注釋》。以后又有巴歇(Bachet de Méziriac，1581—1638)校訂注釋的希臘-拉丁文對照本《亞歷山大的丟番圖算術6卷，多角數1卷》。

丟番圖享年之謎

在《希臘詩文選》中，收錄了一個特別有趣的丟番圖墓志銘： 

用這樣的方式記載了他享年的秘密，即“丟番圖的一生，童年生活占1/6 ，再過1/12 他開始長胡子，再過1/7 他結了婚，婚后 5 年生了一個兒子。他的兒子比他早 4 年辭世，享年是他的1/2 。”
這相當于一元一次方程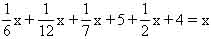： x=84。由此知他享年84歲。