|
1859年,黎曼發表了《在給定大小之下的素數個數》的論文。這是一篇不到十頁的內容極其深到的論文,他將素數的分布的問題歸結為函數的問題,現在稱為黎曼函數。黎曼證明了函數的一些重要性質,并簡要地斷言了其它的性質而未予證明。
在黎曼死后的一百多年中,世界上許多最優秀的數學家盡了最大的努力想證明他的這些斷言,并在作出這些努力的過程中為分析創立了新的內容豐富的新分支。如今,除了他的一個斷言外,其余都按黎曼所期望的那樣得到了解決。
現在來說黎曼猜想,在1858年黎曼寫的一篇長度只有8頁的關于素數分布的論文,在這篇論文中,他提出了有名的黎曼猜想。這猜想提出已有一百多年了,許多有名的數學家曾嘗試去證明,就像喜歡爬山的人希望能爬上珠穆朗瑪峰一樣——因為它的頂峰非常困難到達,目前已有人登上這世界高峰,可是卻沒有人能證明這猜想!
要想說明黎曼猜想,首先要講講這個問題的來源。幾千年前人類就已知道2,3,5,7,31,59,97這些正整數。除了1及本身之外就沒有其他因子,他們稱這些數為素數(或質數),希臘數學家歐幾里得證明了在正整數集合里有無窮多的素數,他是用反證法證明,可以參看《數學和數學家的故事》第一集里這個證明。著名的瑞士數學家歐拉,在1737年給了歐幾里得定理的另外一個巧妙的證明。
人們早知道下面的調和級數是不收斂(即和是無窮大)。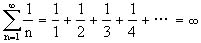
在1737年左右歐拉引進了齊打函數(Zeta function)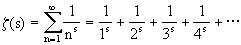
如果令P表示所有的素數集合,即歐拉發現對于S≥1,我們有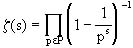 上式的右邊表示 上式的右邊表示
讓p跑遍所有的素數集合,取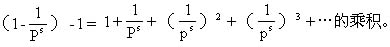 我們看到 我們看到
右邊如果展開,每一項是形如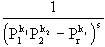 的形狀,這里p1,p2,…,pr都是素數。由算術
的形狀,這里p1,p2,…,pr都是素數。由算術
的基本原理,我們知道,任何正整數是能表示成素數方的乘積,而這表示法是只有一種。如果素數的個數是有限,則當s逐漸趨近于1時,我們見到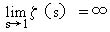 而右邊的結果卻是有限,這樣就
而右邊的結果卻是有限,這樣就
產生了矛盾。由此可知素數的個數不可能是有限的。
在1858年黎曼在他寫的唯一一篇關于數論的文章里把齊打函數的定義域擴大到復數域上,他要研究什么樣的復數s,能使ζ(s)=0,他在文章里給出了下面猜想,現稱為“黎曼猜想”
“所有的非實數的復數s使得ζ(s)=0,,必定在直線Re(s)=1/2 上。”
這個未解決的問題是希爾伯特23個問題中的第8個問題,至今仍沒有人證明。對于某些其它的域
,布爾巴基學派的成員已證明相應的黎曼猜想。數論中很多問題的解決有賴于這個猜想的解決。黎曼的這一工作既是對解析數論理論的貢獻,也極大地豐富了復變函數論的內容。 德國數學家F.克萊因這樣的評價他:“黎曼具有很強的直觀,由這天份他超越了當代的數學家,在他的興趣被激發的領域,他不管是否當局會接受對這研究的肯定,也不讓傳統來誤導他。……他像流星一樣出現然后消失,他活躍的時間只不過15年,1851年他完成論文,1862年他生病,1866年他去世。……黎曼的思想,對現代函數論發展的影響是緩慢和逐漸的,他的工作不會在當代引起突然的革命。這主要是由于黎曼的工作是不容易明白,另外是他提出的想法是非常新且奇特的。……”
黎曼的工作直接影響了19世紀后半期的數學發展,許多杰出的數學家重新論證黎曼斷言過的定理,在黎曼思想的影響下數學許多分支取得了輝煌成就。
近年對黎曼假設的研究
荷蘭三位數學家J.van de Lune,H.J.Riele te及D.T.Winter利用電子計算機來檢驗黎曼的假設,他們對最初的二億個齊打函數的零點檢驗,證明黎曼的假設是對的,他們在1981年宣布他們的結果,目前他們還繼續用電子計算機檢驗底下的一些零點。在1982年11月蘇聯數學家馬帝葉雪維奇在蘇聯雜志《Kibernetika》宣布,他利用電腦檢驗一個與黎曼猜想有關的數學問題,可以證明該問題是正確的,從而反過來可以支持黎曼的猜想很可能是正確的。
|

